Music theory is the foundation of every hit song. This guide explains fundamental music theory concepts like pitch, notes, intervals, major and minor keys, chords, and chord progressions. We'll be exploring how you can use these concepts to write more musical songs.
Some music producers may come from a musical background, while others may not. It’s quite common for people to grow up playing piano or guitar, but this doesn’t guarantee a sufficient understanding of music theory. This guide will cover essential music theory for music producers, and help you wrap your head around some fundamental concepts that every music producer must be aware of.
I run into people online all the time saying that you don’t need to know about music theory to write music. This is true, but knowing about music theory is going to allow you to write music faster and more efficiently; this doesn’t guarantee the music you write will be objectively “better,” but it will absolutely open a world of creative possibilities.
To some degree, limitation breeds ingenuity. When it comes to plugins, finding yourself a great plugin bundle for producers and learning how to use the included tools inside and out is critical. Limiting yourself to a set of devices that you’re familiar with is a great idea, but this concept often gets misconstrued and applied to music theory in the worst way imaginable. Having no understanding of music theory is like having no mixing or mastering tools. Being limited to nothing is not the same as being limited to something.
Music theory is usually taught to kids when they’re young, so many of the music theory resources available don’t really explain the scientific reasoning behind why things are the way they are. Hardly anything involving music theory is arbitrary; there’s reasoning, logic, and even mathematics behind what initially seems like chaos. I hope that by the end of this guide you’ll have a good understanding of pitch, notes, intervals, major/minor keys, and various types of chords. You should also be able to confidently write chord progressions within your DAW.
Pitch
Every sound has a distinct pitch that allows you to tell if it’s “higher” or "lower” than other sounds. The frequency of a sound is measured in hertz (Hz), or cycles per second and the range of human hearing is roughly 20-20,000 Hz. A sine wave resonating at 175 Hz is going to sound “lower” than a sine wave resonating at 1750 Hz. Frequency can be viewed on a spectrum analyzer like the PAZ Analyzer; all of the information that shows up on the graph contributes to how you perceive pitch.
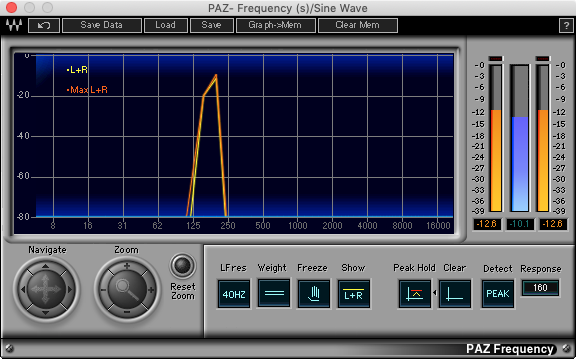
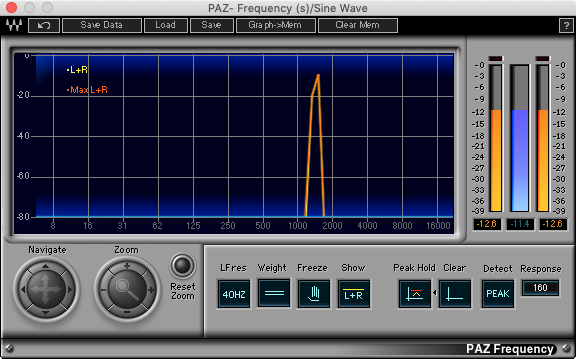
Even sounds that have a more complex harmonic structure than a sine wave can produce a pitch; this is because pitch is something that’s perceived. When you pluck a guitar string, the string resonates, and the sound is amplified via the body of the guitar. The fundamental frequency at which the string resonates dictates pitch, along with its harmonic overtone series; these are the peaks that appear in the spectrum analyzer. When you see a guitarist press down on a string with their finger, what they’re doing is actually increasing the frequency at which the string is vibrating, making the pitch higher.

Notes
Specific frequencies have assigned letter values such as C, C#/Db, D, D#/Eb, E, F, F#/Gb, G, G#/Ab, A, A#/Bb, and B; in total there are 12 of these letters, which we commonly refer to as notes. Notes allow us to identify different frequencies and communicate this information to other music producers and musicians. The following image is a note frequency chart that indicates the letter names that correspond to various frequencies.
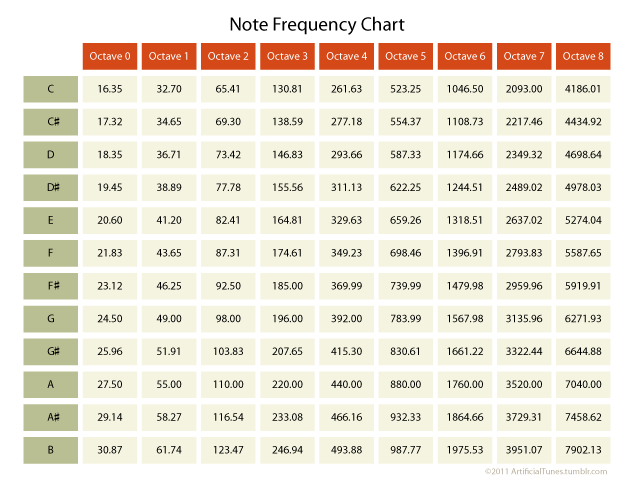
As you may have noticed in the note frequency chart, each letter is assigned to multiple frequencies. Slightly less obvious is the fact that every frequency on the chart is somehow related to the frequencies that surround it.
Let’s use 440 Hz as an example, which is the A in the 4th-octave column. The frequency an octave below A is 220 Hz, which is half of 440 Hz. The frequency an octave above A is 880 Hz, which is twice that of 440 Hz. The frequency a single letter value below (in terms of Hz) 440 Hz is 415.30 Hz, which is 0.9438636 times that of 440 Hz. The frequency above (in terms of Hz) 440 Hz is 466.16 Hz, which is 1.0594545 times that of 440 Hz.
You can use the stated calculations to determine the frequency of notes surrounding any given frequency with an assigned letter value. Just remember that these frequencies aren’t random; they’re mathematically related to one another. The next section will explain this concept in even more detail.
On a piano keyboard, every white key and black key is assigned a note name. The sound they play never changes, but they're sometimes referred to by alternative names based on the key of the song you're writing (more on this later). For example, C# may sometimes be referred to as Db. The following video by Liberty Park Music does a great job of explaining naming notes further.
A 440 Hz
A 440 Hz is a rather unique frequency because it’s used as a general tuning standard for musical pitch. Every frequency on the Note Frequency Chart is based on A 440 Hz. Before this frequency was standardized, other frequencies were used as the tuning standard. In the past, 435 Hz was quite popular, which meant that the frequency of every additional note was different as well.
This relative relationship between notes means that they aren’t just arbitrary frequencies; this has a tremendous impact on what we’re able to do with musical notes. Some of these things include the ability to transpose notes up/down one or more octaves, as well as develop a sense of relative pitch. With a refined sense of relative pitch, you’re able to identify musical intervals by ear, which can allow you to transcribe melodies and chord progressions quickly.
Intervals
You saw in the note frequency chart that doubling the frequency of a note jumped up an octave while the letter remained the same, and halving the frequency of a note jumped down an octave while the letter remained the same. An octave is what is known as an interval.
There are 13 intervals that you’ll want to memorize. Each interval refers to the difference in pitch between two sounds. In a more practical sense, these intervals may refer to the difference in pitch between two notes on your keyboard:
- Unison: Equivalent in pitch
- Minor 2nd: 1 semitone difference in pitch
- Major 2nd: 2 semitone difference in pitch
- Minor 3rd: 3 semitone difference in pitch
- Major 3rd: 4 semitone difference in pitch
- Perfect 4th: 5 semitone difference in pitch
- Tritone: 6 semitone difference in pitch
- Perfect 5th: 7 semitone difference in pitch
- Minor 6th: 8 semitone difference in pitch
- Major 6th: 9 semitone difference in pitch
- Minor 7th: 10 semitone difference in pitch
- Major 7th: 11 semitone difference in pitch
- Octave: 12 semitone difference in pitch
The cool thing about intervals is that you can move them around your keyboard, and they’ll still be the same interval. Again, this is another way in which music revolves around the concept of relativity. The specific notes you play on your keyboard are somewhat irrelevant. What matters is the number of semitones between the notes. An interval played on its own, should “feel” similar regardless of where you play it on your keyboard.
Major and Minor Keys
Now that I’ve loaded you up with a healthy amount of information, you’re probably wondering what to do with it. In music, certain groups of notes form what is known as a key, and these notes tend to sound subjectively good when played with one another. The key of a song is partially responsible for the feelings it evokes. For example, major keys tend to sound rather happy, while minor keys tend to sound rather sad.
A key is made up of a root note, and a set of intervals. For example, a major key consists of a root note, major 2nd, major 3rd, perfect 4th, perfect 5th, major 6th, major 7th, and an octave. To create a major key, select a note on your keyboard (which will act as the root note), and count semitones to figure out the remaining notes that fall within that key.
Instead of counting individual semitones from the root note, you can use the formula WWHWWWH to count semitones faster. “W” represents a step of 2 semitones, while “H” represents a step of 1 semitone. Starting at the root note, you would count up 2 semitones, then another 2 semitones, then 1 semitone, etc. If you’re starting on C, and you do this correctly, you’ll end up with the following highlighted notes.
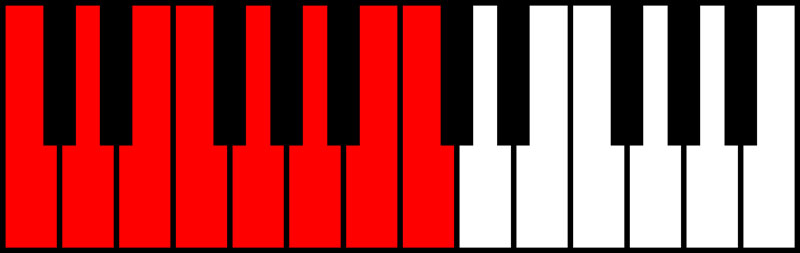
This is what C major sounds like played up and down the keyboard using the Waves Electric 88 Piano:
The same concept applies to building a minor key. In a minor key, the major 3rd is dropped down to a minor 3rd, the major 6th is dropped down to a minor 6th, and the major 7th is dropped down to a minor 7th. The formula for this is WHWWHWW.

This is what C minor sounds like played up and down the keyboard using the Waves Electric 88 Piano:
Notice how C major sounds kind of happy, whereas C minor sounds kind of sad? This is a perfect example of how certain keys evoke certain emotions.
These WWHWWWH and WHWWHWW formulas work for keys other than just C major and C minor. If you select a different root note, like F, you can create the key of F major and F minor using the exact same formulas.
The Key of F Major
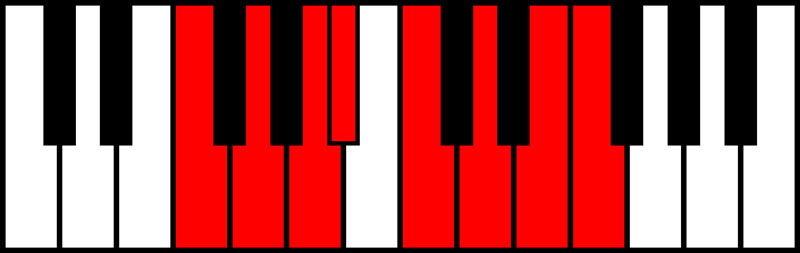
The Key of F Minor

How to Write Chord Progressions
A chord is created when you play two or more notes at the same time. Chords that contain two notes are called diads, while chords that contain 3 notes are called triads. When you play a simple 2 note interval, you’re playing a diad.
Some extremely common piano chords include major chords, minor chords, and diminished chords, which are all triads. They’re created using the following formulas:
- Major Chord: Root, Major 3rd, Perfect 5th
- Minor Chord: Root, Minor 3rd, Perfect 5th
- Diminished Chord: Root, Minor 3rd, Tritone (Diminished 5th)
C Major Chord
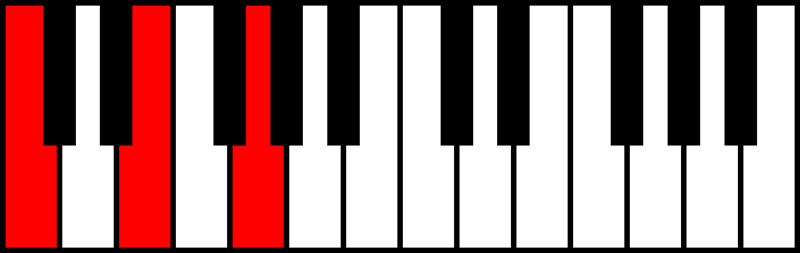
C Minor Chord
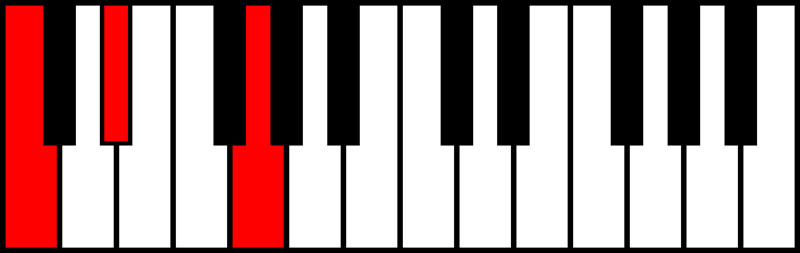
C Diminished Chord

Major keys and minor keys contain an assortment of triads. You can try to figure out which chords fit inside the key you’re working with, or you can use yet another simple formula. Let’s take another look at major and minor keys to figure out how to do this. Watch the following video by PianoPig to learn more about creating chords.
Each note within a major and minor key can be assigned a scale tone number. This allows us to talk about notes in a relative sense, without having to use their specific note name. Since major and minor keys are based on the root note that you select, this is quite ideal. We’re able to avoid diving into the specifics of one particular key and talk about music theory in a more general, transferable sense.
Scale Tones for C Major
Scale Tones for F Major
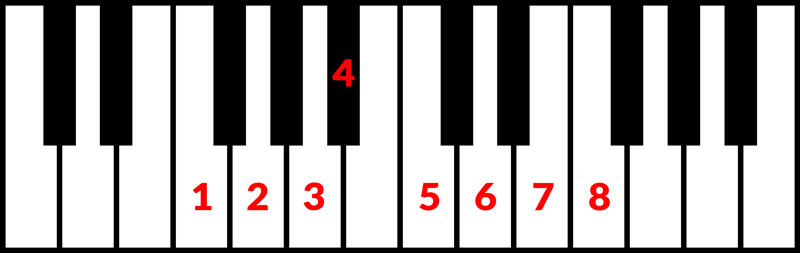
In a major key, each scale tone has a chord that corresponds to it, using the scale tone number as the root note:
- 1 = Major Chord
- 2 = Minor Chord
- 3 = Minor Chord
- 4 = Major Chord
- 5 = Major Chord
- 6 = Minor Chord
- 7 = Diminished Chord
- 8 = The Pattern Repeats
In a minor key, each scale tone has a chord that corresponds to it as well, using the scale tone number as the root note:
- 1 = Minor Chord
- 2 = Diminished Chord
- 3 = Major Chord
- 4 = Minor Chord
- 5 = Minor Chord
- 6 = Major Chord
- 7 = Major Chord
- 8 = The Pattern Repeats
At this point, you know everything you need to start writing chord progressions. To create a basic four-chord progression, select whether you want to write in a major or minor key, pick four scale tones, and then match them to their corresponding chords. Seems pretty simple, right? Well, it is!
There are plenty of common chord progressions that you can look up online. Typically, they’re written using Roman numerals. For example, I–V–vi–IV (1-5-6-4) is a common major key progression. To make things even easier, the upper case Roman numerals are major chords, while the lower case Roman numerals are minor chords. The symbol ° is used to indicate diminished chords.

Underbelly from You Suck at Producing has a great video on writing chord progressions in Ableton Live. Even if you already know how to write chord progressions, the video is good for a couple laughs.
Take what you’ve learned and start experimenting with writing chord progressions. There’s a lot of information to absorb here, so make sure to bookmark this page and refer back to it if you need to. To progress your understanding of music theory further, I recommend you checkout Hooktheory. It's a website that offers software, books, tabs, and videos on writing music.
Want to produce radio-quality songs? Check out Black Ghost Audio's Music Production for Beginners video course. Produce three songs from start to finish and learn the skills you need to write, record, mix, and master music at home. No experience required. Click here to learn more and produce your first song in under an hour.

















